

Origines des figures impossibles
Avant le XXe siècle
En 1754, William Hogarth, peintre et graveur anglais du XIX siècle, publie une gravure sur cuivre intitulée « False perspective » dans laquelle il montre aux dessinateurs de l’époque les erreurs de perspective à ne pas commettre.
Au XXe siècle
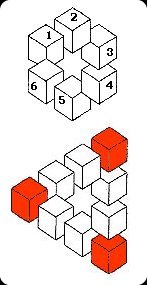 C’est en 1934
qu’Oscar Reutersvärd dessine, par hasard, la première figure impossible sous la forme d’un
triangle ! Après avoir dessiné une étoile à six branches et entouré
C’est en 1934
qu’Oscar Reutersvärd dessine, par hasard, la première figure impossible sous la forme d’un
triangle ! Après avoir dessiné une étoile à six branches et entouré
 celle-ci de six cubes (1 à 6), il en ajoute trois autres (les cubes rouges) pour obtenir une forme triangulaire.
Cette première figure « paradoxale » a
été suivie de plus de 2500 dessins d’objets impossibles !
celle-ci de six cubes (1 à 6), il en ajoute trois autres (les cubes rouges) pour obtenir une forme triangulaire.
Cette première figure « paradoxale » a
été suivie de plus de 2500 dessins d’objets impossibles !
Un quart de siècle plus tard (1958), Roger Penrose, un mathématicien anglais, réinvente ce triangle impossible, qui portera désormais son nom.
La même année, Escher connaît un grand succès en publiant une image du cube de Necker. Il est le premier à dessiner un « cube impossible ». Parmi son œuvre immense, Escher a créé quatre tableaux représentant des objets impossibles : « Concave et convexe », « Belvédère », « Montant et descendant » et « Cascade ».
Les objets impossibles

 L’une des questions les plus intéressantes en rapport avec les objets impossibles
est celle-ci : « Existent-ils ou n’existent-ils pas ? » Si
l’on se contente d’un dessin de l’objet, il ne fait aucun doute que celui-ci
existe bel et bien ; mais, dès que l’on quitte la feuille plane pour se
transporter dans le véritable monde à trois dimensions dans lequel nous vivons,
la question reprend tout son sens, puisqu’il semble impossible d’y retrouver
l’objet tel qu’il a été dessiné. C’est la raison pour laquelle nous
parlons ici d’objets impossibles, et non de figures impossibles.
L’une des questions les plus intéressantes en rapport avec les objets impossibles
est celle-ci : « Existent-ils ou n’existent-ils pas ? » Si
l’on se contente d’un dessin de l’objet, il ne fait aucun doute que celui-ci
existe bel et bien ; mais, dès que l’on quitte la feuille plane pour se
transporter dans le véritable monde à trois dimensions dans lequel nous vivons,
la question reprend tout son sens, puisqu’il semble impossible d’y retrouver
l’objet tel qu’il a été dessiné. C’est la raison pour laquelle nous
parlons ici d’objets impossibles, et non de figures impossibles.
La question est donc : peut-on réaliser un objet impossible correspondant
à une figure impossible ? Stricto sensu, la réponse est
« Non » !, mais il est possible d’atteindre une forme plus ou moins
réaliste de l’objet. Jusqu’à présent, les deux seules approches imaginées pour
leur réalisation présentaient des inconvénients majeurs, dont le principal était
qu’il fallait se placer à un point précis pour observer l’objet si l’on
voulait le voir dans toute son
« impossibilité ». Il existe ainsi deux sculptures, toutes deux monumentales, du
célèbre triangle impossible de Reutersvärd : la première est à
Perth, en Australie ; c’est une sculpture « ouverte » ; la seconde
se trouve à Ophoven, en Belgique ; c’est un triangle « en vrille »,

 néanmoins très esthétique ! Mais, dans un cas comme dans l’autre, seuls des observateurs
initiés aux objets impossibles peuvent les voir comme des triangles, les autres n’y voyant que des sculptures
abstraites.
néanmoins très esthétique ! Mais, dans un cas comme dans l’autre, seuls des observateurs
initiés aux objets impossibles peuvent les voir comme des triangles, les autres n’y voyant que des sculptures
abstraites.
Actuellement, Francis Tabary est le seul à avoir réussi à rendre en trois dimensions une figure qui semblait à jamais condamnée à la planéité de la feuille de papier, et à rendre cet objet, apparemment impossible, visible par n’importe qui, même un non-initié. L’objet n’est ni vrillé ni ouvert, et non seulement il peut être vu dans toute sa gloire d’objet impossible par tout observateur placé devant, mais en plus il semble acquérir des propriétés cinétiques lorsque celui-ci se déplace sans le quitter des yeux. C’est un subtil jeu d’ombres et de lumières, créé naturellement par la lumière du jour ou une source de lumière artificielle, qui lui donne son volume et le rend « réel ».
Les ambigrammes
Qu’est-ce qu’un ambigramme ?
Un ambigramme (ou inversion) est une graphie d’un mot qui, vue sous un certain angle ou après rotation, donne soit le même mot, soit un mot différent. Il s’agit avant tout d’un exercice de calligraphie où la maîtrise des illusions d’optique et des symétries joue un rôle essentiel.
Les différents types d’ambigrammes
-
Les ambigrammes simples
Le mot reste le même après avoir subi une rotation de 180°.
Exemples :
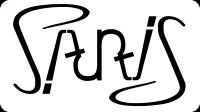
PARIS sera toujours PARIS 
ART reste ART 
LOVE reste LOVE -
Les ambigrammes doubles
Un mot se transforme en un autre mot après rotation, tout l’intérêt résidant évidemment dans le lien sémantique ou autre entre les deux mots.
Exemples de rotation centrale de 180° :
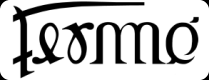
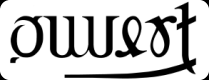
Fermé devient Ouvert 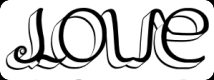

Love devient amor (voir sculpture) Une rotation axiale verticale ou horizontale peut également offrir des possibilités intéressantes.
Exemples de rotation de 180° suivant l’axe vertical :


Tabary se transforme en Francis 

Design by devient Ph. Starck Exemples de rotation de 180° suivant l’axe horizontal :
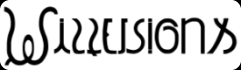
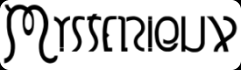
Les illusions donne mystérieux 
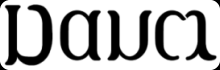
Nancy se transforme en Daum
Les créateurs d’ambigrammes
Les pionniers dans ce domaine sont Scott Kim et Douglas Hofstadter, mais vous trouverez beaucoup d’autres sites de créateurs sur Internet.
L’utilisation des ambigrammes par Francis Tabary
Les ambigrammes peuvent jouer un rôle intéressant dans la publicité, à condition de trouver un support adéquat qui les mette en valeur. Présentés sous forme de sculptures, ils ajoutent à celles-ci un côté magique et ambivalent.
Un grand nombre d’ambigrammes créés par Francis Tabary vont bientôt voir le jour. Rendus possibles par l’utilisation de supports transparents, de projections d’ombres et d’effets de miroir, ils illustrent une autre facette, tout aussi passionnante, de l’art magique de Francis Tabary. À découvrir bientôt sur ce site !











